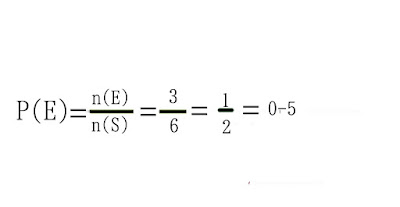Ejercicio.4

 Problemas de Probabilidad 

Desviación Típica

Cálculo de la desviación media y desviación típica:

Media Aritmética

Aplicación de la fórmula para el cálculo de la media aritmética :

Ejercicio 1

Desarrollo de un ejemplo de tipos de frecuencias:

Conceptos básicos, variables, medidas

https://www.youtube.com/watch?v=nJF7ouvoIXI

Variables y su clasificaciòn

Variables

Variable estadística: al conjunto de distintos valores numèricos que adopta un caracter cuantitativo se divide en dos grupos:

• Cualitativas o categóricas:
  

  No se pueden medir numéricamente por ejemplo: el color de piel, nacionalidad.

• Cuantitativas: 

        Tienen valor numérico, por ejemplo: la edad de una persona, precio de un producto, etc. Se clasifican en :

              Discretas: sólo pueden tomar valores enteros (2,4,6,8).

              Continuas: pueden tomar cualquier valor real dentro 

              de un  intervalo (2,5;6.4), por ejemplo: la velocidad

              de una motocicleta puede ser 105.3km/h

Variables unidimensionales: solo recogen información sobre una caracteristica, ejemplo: la altura.

Variables bidimensionales: recogen información sobre dos caracteristicas de la poblaciòn, ejemplo: la altura y la edad.

Variables pluridimensionales: recogen información de tres o mas caracteristicas de la población, ejemplo: la altura, edad, sexo, peso, etc.

 

 

Probabilidad clasica

Probabilidad clásica

Es el número de resultados favorables a la presentación de un evento dividido entre el número total de resultados posibles. Asignación de probabilidad "a priori", si necesidad de realizar el experimento. 

La probabilidad clásica o teórica se aplica cuando cada evento simple del espacio muestral tiene la misma probabilidad de ocurrir.

(Rafael Díaz. 2000)

Fórmula para obtener la probabilidad clásica o teórica:

Ejemplo: 

¿Cuál es la probabilidad de obtener un número mayor que 3, en el lanzamiento de un dado? 

Si E: 4, 5, 6, entonces el número de resultados favorables es n (E) = 3.
Si S: 1, 2, 3, 4, 5, 6, entonces el número total de resultados posibles es (S) = 6.

Por lo tanto:

Esta definición clásica de probabilidad fue una de las primeras que se dieron (1900) y se atribuye a Laplace; también se conoce con el nombre de probabilidad a priori pues, para calcularla, es necesario conocer, antes de realizar el experimento aleatorio, el espacio muestral y el número de resultados o sucesos elementales que entran a formar parte del suceso.

(Rafael Díaz. 2000) 

La aplicación de la definición clásica de probabilidad puede presentar dificultades de aplicación cuando el espacio muestral es infinito o cuando los posibles resultados de un experimento no son equiprobables.(Rafael Díaz. 2000) 

Ejemplo:

En un proceso de fabricación de piezas puede haber algunas defectuosas y si queremos determinar la probabilidad de que una pieza sea defectuosa no podemos utilizar la definición clásica pues necesitaríamos conocer previamente el resultado del proceso de fabricación.

Para resolver estos casos, se hace una extensión de la definición de probabilidad, de manera que se pueda aplicar con menos restricciones, llegando así a la definición frecuentista de probabilidad: